1.0 with a number of game ( Fun with numbers),
Before learning about the properties of numbers , let us know some interesting things about them.
Did you say the number that came to mind?
Can you tell the number your friend kept in his mind?
Follow the steps below :
Ed.
|
Action.
|
E.g.
|
1
|
Tell your friend to have a full number in mind
|
Let 27 be
|
2
|
Multiply it by 2
|
54
|
3
|
Tell them to add 4 to it
|
58
|
4
|
Tell it to divide by 2
|
29
|
5
|
Tell them the answer
|
29
|
If the answer is 2, then the number he has in mind is 27!
What is the math behind this ?
Let x be a number .
Ed.
|
Action
|
E.g.
|
1
|
Ask your friend to keep a full number in mind
|
Let x be
|
2
|
Multiply it by 2
|
2x
|
3
|
Tell them to add 4 to it
|
2x + 4
|
4
|
Tell it to divide by 2
|
x + 2
|
5
|
Tell them the answer
|
x + 2
|
The number that comes from that answer is 2 , the number he has in mind is x
Similarly, think of your own formula (eg multiply by 4 , .....)
In mathematics, there are many such tricks that can be tailored to your imagination.
The number of 1 to 9, plus special numbers .
1. The sum of the digits of the number 123456789 is 45 (= 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9)
2. The number multiplied by 2 is 246913578. The sum of the digits in this number is 45 (= 2 + 4 + 6 + 9 + 1 + 3 + 5 + 7 + 8) . Another point to note here is that each of the numbers from 1 to 9 is non-repetitive! What do you notice by multiplying 123456789 by 4,5,7,8 ?
3. Note the multiples of 9 (they are : 9, 18, 27, 36, 45, 54, 63, 72, 81, 90,99,108,117 .. ( The sum of the digits of these is 9 (1 + 8 = 9,2 + 7 = 9). .) Note also that.
Categories features :
What did you notice?
A number class is obtained by adding an odd number that is sequential to the number of the previous class.
Wondering? There is a mathematical formula behind this. In the next lessons we will learn how to expand (a + b) 2 . As such
(n + 1) 2 = n 2 + 2n + 1 2 = n 2 + (2n + 1).
Where 2n + 1 is the next odd number of the last odd number in n 2 .
Meru Proposal: Note the following alignment :
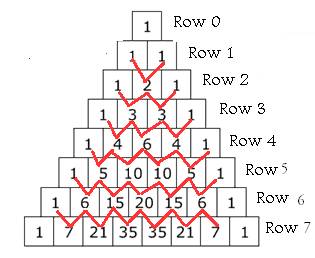
This is the first tip of the triangular caukadolagina the number of victims in the film 1 in which the Row 0 agideyavude the final two on each side of the square adjacent to the number 0 for other meanings. Row 1 line caukadolagina digits 1 and 1 to Ve . This is the sum of 1 and 0 in the square above it . The number in the square of Row 2 is 1,2,1 , which is the sum of 0,1, 1,1 and 0,1 , respectively . (0 + 1 = 1 ; 1 + 1 = 2 ; 1 + 0 = 1 ). Row 3 line Square No. 1,3,3,1 , respectively, its upper square 0,1, 1,2,2,1 and 0.1 of the sum . (0 + 1 = 1 ; 1 + 2 = 3 ; 2 + 1 = 3 ; 0 + 1 = 1 ). This is how each row can be filled with numbers. [Simply put, if n is a line number and r is a square number, then every number in the square can be filled with n C r = ]. n C r Next Class 10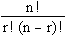 
Learn from. Cree, Poo. 2 century pingalanu used this idea in his chandas science appears to us, is Meru present (stepping on top of the mountain) was called. This is attributed to AD. 10 th century, halayudhanu definition given. Ironically, it was invented by Indians as early as 1900 years ago, but it is still in existence . 17th -century mathematician Pascal 's name is called!
Learn from. Cree, Poo. 2 century pingalanu used this idea in his chandas science appears to us, is Meru present (stepping on top of the mountain) was called. This is attributed to AD. 10 th century, halayudhanu definition given. Ironically, it was invented by Indians as early as 1900 years ago, but it is still in existence . 17th -century mathematician Pascal 's name is called!
Notice the specifics of Pingala's masterpiece .
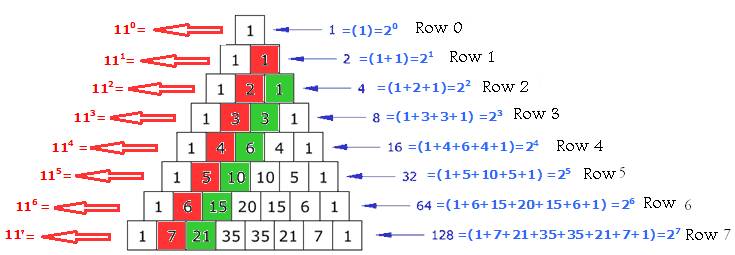
Specials (where of n ( have 0 from the start) line sankhyeyagirali) :
1. caukadolagina the sum of digits is always 2 of n ( blue in color, was identified) ( eg : 1 = 2 0 1 + 1 = 2 = 2, 1 , 1 + 2 + 1 = 4 = 2 2 1 + 3 + 3 + 1 = 8 = 2 3 ,,)
2. The row number is always 11 n ( marked in red ) ( eg 1 = 11 0 , 11 = 11 1 , 121 = 11 2 , 1331 = 11 3 …)
3. The digits in the square of the diagonal denote the natural numbers. (1,2,3…. Red squares )
4. hypotenuse Square digits former vice gathered in the full vargasankhyeyaga be (1 = 1 2 , 1 + 3 = 4 = 2 2 , 3 + 6 = 9 = 3 2 , 6 + 10 = 16 = 4 2 , .... The green -colored squares )
(The square root of two identical numbers is a whole number )
5. Any string 2 in number than any other avibhajyasankhyeyagiddare, that string in the following digits on its gunalabdhagalagiruttave. ( For example, row 3 of the Sun 3,3 : Line 5 in the 5,10,10,5 ; line 7 in 7213535217)
Seeing the above statement in a different way :
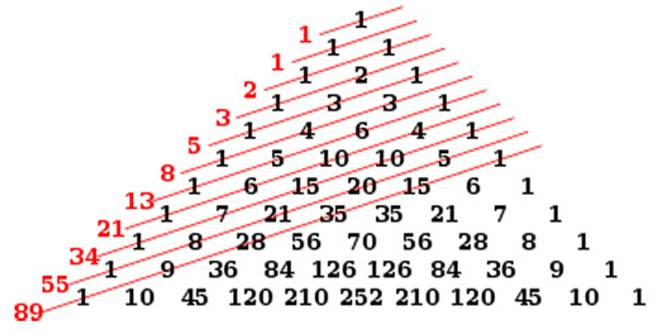
The first 1 to leave a red color on the diagonal numbers indicated in the previous 2 numbers mottavagiruttadeavu
1 2 3 5 8 13 21 34 55 89 ( 2 = 1 + 1, 3 = 2 + 1, 5 = 2 + 3,8 = 3 + 5, 13 = 5 + 8, 21 = 8 + 13, 34 = 13 +21 ..).
This series is called the Italian mathematician Fibonacci ( 12th century).
Magic :
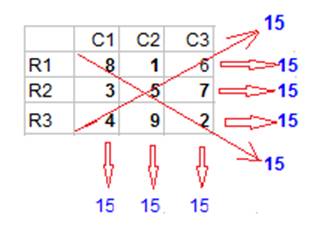
It is a 3 x 3 square and there are 9 squares (3 horizontal lines : R1, R2 and R3). (3 pole lines C1, C2 and C3). The digits in the squares are from 1 to 9 , with no middle point left and none repeating. As well
The sum of the digits of each row ( R1, R2 and R3) is 15.
The sum of the digits of each pole (C1, C2 and C3) is 15.
The sum of the digits of the diagonal line ( drawn from the red line ) is 15.
15 of mayamotta ( ', as Magic in a sum ', ), that kareyutteveadu row / column / sum of digits on the diagonal.
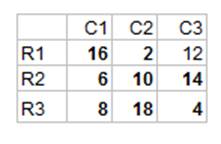
Above is a magic wand that contains all the numbers from 2 to 18 (9 digits ) . Here is the magic amount of 30.
More examples:
5 x 5 magic ( magic = 65)
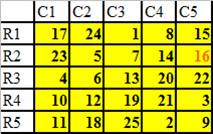
7 x 7 magic ( magic = 175)
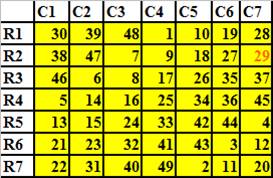
Mayamotta be given to such a magic square is impossible to create ?. Possible and mayamotta 45 have the magic square
So far we have learned about some interesting numbers in mathematics . So what's the math ?
Let us think about solving a business problem
Problem : Your father / mother / relatives pay their friends Rs . Assume that 5000 is lent . After some time , this is the type of debt payment that he will not be burdened with . That day is the day sankhyeganugunavagi 1 crore as of 100 days and amortization ( 1 th Day 1 and Rs 2 on the third day 2 rupees .... The 100 th day of 100- Rs ). If so, can that friend pay off ?How much more / less will he return ?
Here's what we have to do 1 starting from 100 until the calculated sum of the numbers in the hidiyabekallave ?
General and corrective action :
1
+2
+3
+4
… :
+100
====
====
Bahusa : 10 pm kudisuvalli celluvire lost patience with the hand? Is it possible the other way around?
Step 1 :
1 + 2 + 3 + 4 + 5 . . How to write a + 100 in two lines as follows?
1+ 2+ 3 + 4 + 5 … + 50
100+ 99+ 98+. . .. +51
==================
101 + 101 + 101. .. . +101
==================
= 50 * 101 = 5050
Step 2 :
1 + 2 + 3 + 4 + 5 . . . + 10 = 55
11 + 12 + 13 + . . . + 20 = (10 + 1) + (10 + 2) + (10 + 3) +. . . + (10 + 10) = 155
21 + 22 + 23 + . . . + 30 = (20 + 1) + (20 + 2) + (20 + 3) +. . . + (20 + 10) = 255
. . . . . .
91 + 92 + 93 + . . + 100 = (90 + 1) + (90 + 2) + (90 + 3) +. . . + (90 + 10) = 955
Total = 55 + 155 + 255 …… + 955 = 100 + 200… + 900 + 55 * 10 = 100 (1 + 2 + 3…. +9) + 550 = 4500 + 550 = 5050
Step 3 :
1 + 2 + 3 + 4 + 5 . . .9 + 10
1) Average of 1 and 10 = 5.5
2) The mean of 2 and 9 = 5.5
..
5) The mean of 5 and 6 = 5.5
( 1 + 2 + 3 + 4 + 5. 9 + 10) /2=5.5*5= 55( 1 + 2 + 3 + 4 + 5. 9 + 10) = 5.5 * 10 = 55 ( Average * Total Numbers )
The same logic is 1 + 2 + 3 + 4 + 5 . . When used in + 100
Since 1 and 10 0 are average = 50.5 and there are 100 numbers in total
1 + 2 + 3 + 4 + 5 . . . + 100 = 50.5 * 100 = 5050
Note that the answer is the same, although the methods are different. Using a different method saves time. A friend paid Rs . 5000 loan for 100 days, as well as the loan is not fully tirisuvudu hechagi Rs . Gives 50 .
Debt rules help you to solve the problems in exams , especially in competitive (CET , CAT, GMAT, KAS, IAS, Banking, Police ..) tests that are important for time management.
Information Technology Device
|
To be divided into residuals
|
Examples
|
2
|
Last digit must be equal to (0,2,4,6,8)
|
12 8 Yes
12 9 No
|
3
|
The sum of digits in numbers must be divided by 3
|
3 8 1 ( 3 + 8 + 1 = 12, and 12 ÷ 3 = 4) Yes
2 1 7 ( 2 + 1 + 7 = 10, and 10 ÷ 3 in a = 3 in a 1 / 3 in a ), No Do
|
4
|
The last two digits must be divisible by 4
|
13 12 Yes ( 12 ÷ 4 = 3)
70 19 No
|
5
|
Last Digit 0 or 5, the shall
|
17 5 Yes
80 9 No
|
6
|
The number must be divided by 2 and 3
|
1 1 4 ( number , and 1 + 1 + 4 = 6 and 6 ÷ 3 = 2) Yes
3 0 8 ( samasankhyeyadaru , 3 + 0 + 8 = 11 and 11 ÷ 3 = 3 and 2 for / 3 ), No Do
|
7
|
The answer obtained by subtracting the last digit of the number from 2 is subtracted from the remainder
· 0
· Or
To be divided by · 7
( This rule can be applied to the intermediate north of which it is available )
|
67 2 ( 2 's doubled 4, 67 -4 = 63, and 63 ÷ 7 = 9) Yes
6 3 ( 3 's doubled 6, 6 -6 = 0) Yes
90 5 ( 5 of multiples of 10, 90 -10 = 80 and 80 = the 11 of 7 ÷ 3 in a / of 7 ), No Do
|
8
|
The answer obtained by the last 3 digits must be divided by 8 .
|
109 816 ( 816 ÷ 8 = 102) Yes
For 216 in total of 302 ( total of 302 ÷ the 8 = 37- 3 in a / 4 for ), No Do
|
9
|
The sum of digits in the number must be divided by 9 ( this rule can be applied to the answer of the given interval )
|
1 6 2 9 ( 1 + 6 + 2 + 9 = 18, and re : 1 + 8 = 9) Yes
2013 (2 + 0 + 1 + 3 = 6) No
|
10
|
The last digit is 0
|
22 0 Yes
22 1 No
|
11
|
( Sum of digits in equal positions - Sum of digits in odd positions )
0
Or
Divided by 11
|
1 3 6 4 (( 3 + 4 ) - ( 1 + 6 ) = 0 ) Yes
3 7 2 9 (( 7 + 9 ) - ( 3 + 2 ) = 11 ) Yes
2 5 1 7 6 (( 5 + 7 ) - ( 2 + 1 + 6 ) = 3 ) No
|
12
|
The number must be divisible by 3 and 4
|
6 4 8 ( 3 from ? 6 +4+ 8 = 18 and 18 ÷ 3 = 6 Yes 4 from ? 4 8 ÷ 4 = 12 Yes) Yes
5 2 4 ( 3 pm ? 5 +, 2 +, 4 = the 11, the 11 ÷ 3 = 3 2 / 3 No Do 4 pm - check .), No Do
|
1.0 Summary learned
Number
|
Highlights learned
|
1
|
Meru proposal.
Different types of magic
|
2
|
Terms of Indemnity
|
कोणत्याही टिप्पण्या नाहीत:
टिप्पणी पोस्ट करा